ClipUp: A Simple and Powerful Optimizer for Distribution-based Policy Evolution

December 8, 2020

by Nihat Engin Toklu, Paweł Liskowski and Rupesh Kumar Srivastava

⊕
A neural network trained to control the PyBullet Humanoid using PGPE for gradient estimation and ClipUp for optimization.

ClipUp is a simple adaptive optimizer that makes it easier to solve certain optimization problems in practice. It is generally applicable, but is designed to be specially useful for distribution-based policy search algorithms such as PGPE [1], ARS [2] and OpenAI-ES [3] by helping in finding good hyperparameters quickly and intuitively. The technique is simple: use normalized gradient descent with momentum, and clip the parameter updates (not gradients!).

Read the full report on arXiv, extending our PPSN 2020 paper.

Get our code on GitHub, which provides a clean and scalable implementation of PGPE and makes experimenting with this family of algorithms easy.

Algorithm

⊕Notice that by setting the hyperparameters appropriately, we recover normalized gradient descent. The hyperparameters help us control the algorithm behavior in non-idealized conditions. To get straight to the point, the algorithm is given below. Using the metaphors of “heavy-ball” momentum, it computes a new velocity of a ball from the current velocity and gradients, that is then added to the current position to obtain the next position.

⊕Bold symbols denote vectors. \(\textbf{Initialization: } \text{Velocity } \boldsymbol{v_0} = \boldsymbol{0}\)
\(\textbf{Hyperparameters: }\)
\(\text{Step size } \alpha, \text{Maximum speed } v^{\text{max}}, \text{Momentum } m\)
\(\textbf{Input: } \text{Estimated gradient } \nabla f(\boldsymbol{x}_k)\)

\(\text{// }\textit{Velocity update with normalized gradient}\)
\(\boldsymbol{v'}_{k+1} \gets m \cdot \boldsymbol{v}_k + \alpha \cdot \big( \nabla f(\boldsymbol{x}_k) \,/\, ||\nabla f(\boldsymbol{x}_k)|| \big)\)
\(\text{// }\textit{Clip velocity based on norm}\)
\(\text{if } ||\boldsymbol{v'}_{k+1}|| > v^{\text{max}}\)
\(\quad\) \(\boldsymbol{v}_{k+1} \gets v^{\text{max}} \cdot \big( \boldsymbol{v'}_{k+1} \,/\, ||\boldsymbol{v'}_{k+1}|| \big)\)
\(\text{else }\)
\(\quad\) \(\boldsymbol{v}_{k+1} \gets \boldsymbol{v'}_{k+1}\)
\(\textbf{Return: }\boldsymbol{v}_{k+1}\)

ClipUp comes with a strategy for setting and tuning hyperparameters for control problems. Start by setting \(m=0.9\) and \(\alpha=v^{\text{max}}/2\),\(\alpha\) serves as the initial speed at the first iteration and the rate at which velocity changes after that. which leaves \(v^{\text{max}}\) as the main hyperparameter to tune. Next, use \(v^{\text{max}}\) to determine a key hyperparameter of PGPE: \(\boldsymbol{\sigma}\), the initial standard deviation of Gaussian noise used for estimating the gradient. \(||\boldsymbol{\sigma}||\) and \(v^{\text{max}}\) have the same “type”They are Euclidean distances in parameter space. so we recommend tuning their ratio instead. Based on experiments with several environments, we have found that ratios between 10 to 20 work well as a starting point. If computational resources are limited, tune only \(v^{\text{max}}\), otherwise tune the multipliers above for improvements in performance.We recommend tuning the \(||\boldsymbol{\sigma}||/v^{\text{max}}\) ratio, the \(\alpha\) multiplier and \(m\), in order. See Section 4 of our paper to understand how these hyperparameters can be interpreted and how their values are related to each other.

Why ClipUp?

During our experiments with continuous control tasks, we noticed that adjusting hyperparameters often felt like tweaking knobs whose impact on algorithm behavior we couldn’t easily predict.Experiments in our paper use representative tasks based on the MuJoCo and PyBullet physics simulators, but this is a general issue we have faced during practical applications of RL algorithms. When tackling high-dimensional non-convex optimization problems, it is not sufficient to know that an optimizer has good theoretical properties with some ideal hyperparameter settings, since this does not take into account the typical workflow a practitioner might have when solving a problem. This workflow usually consists of starting with default hyperparameter settings of the optimizer, and then attempting to adjust both these values and the remaining hyperparameters of the method to improve results. Many practitioners do not have access to, or can not allocate a large amount of computational resources to perform a large automated hyperparameter search.

Some Desirable Properties of Optimizers

From the perspective of optimizers as components of a problem solving strategy, we consider some questions that a practitioner might ask before deciding to use an optimizer.

Q1: Are there reasonably good default settings for the hyperparameters, that often provide a good starting point for my problem class?

Q2: Can I intuitively interpret the effects of adjusting hyperparameters on the optimizer behavior?

Q3: Are there interpretable relationships between hyperparameters, that help me understand how some hyperparamters should be set in comparison to others?

Q4: Does the optimizer have robustness to variations in problem definition, such as different reward functions that I might experiment with for a given task?

We have found that for ClipUp, the answer to these questions is yes, more so than other common optimizers. As a result we can often quickly configure it to learn successful policies. In particular, it is a great fit for distribution-based search because its hyperparameters can be intuitively interpreted in context of the sampling-based policy gradient estimation algorithm.We used PGPE, but the arguments apply to any Evolutionary or Randomized Search strategy based on related principles.

Summary of Results

Our paper explains how these useful properties of ClipUp arise and presents several results on a range of simulated continuous control benchmarks, including the challenging PyBullet Humanoid. The highlights are summarized by the following plots, all using 30 runs aggregated for comparison:

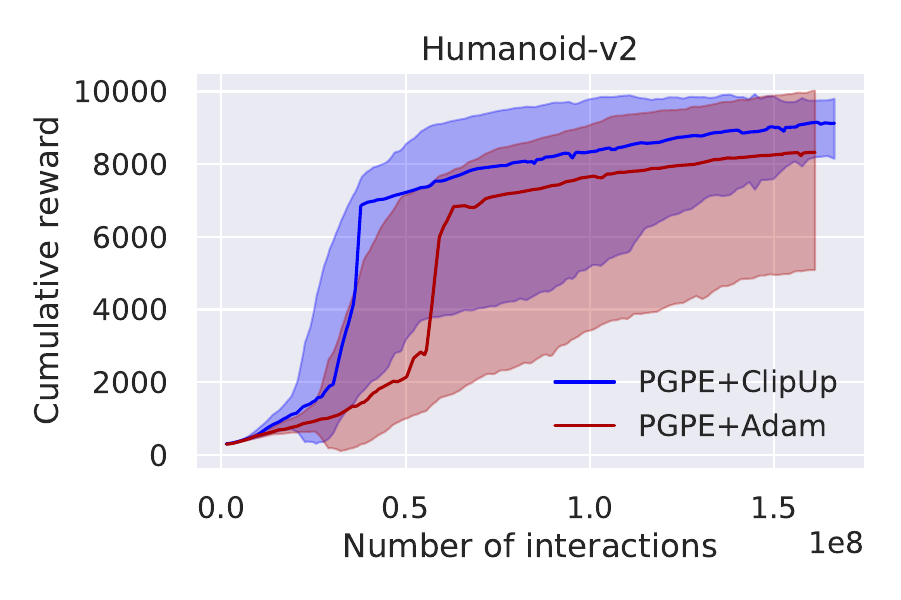
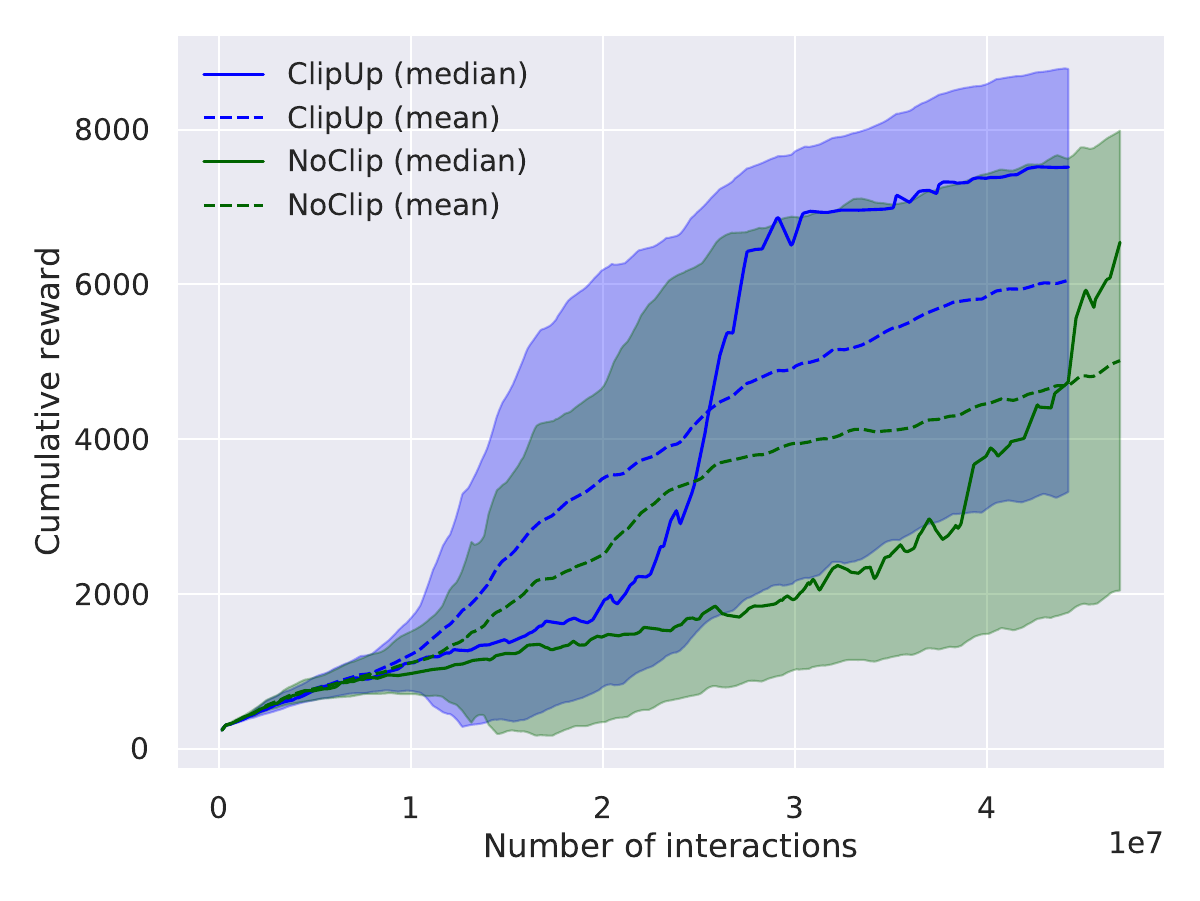
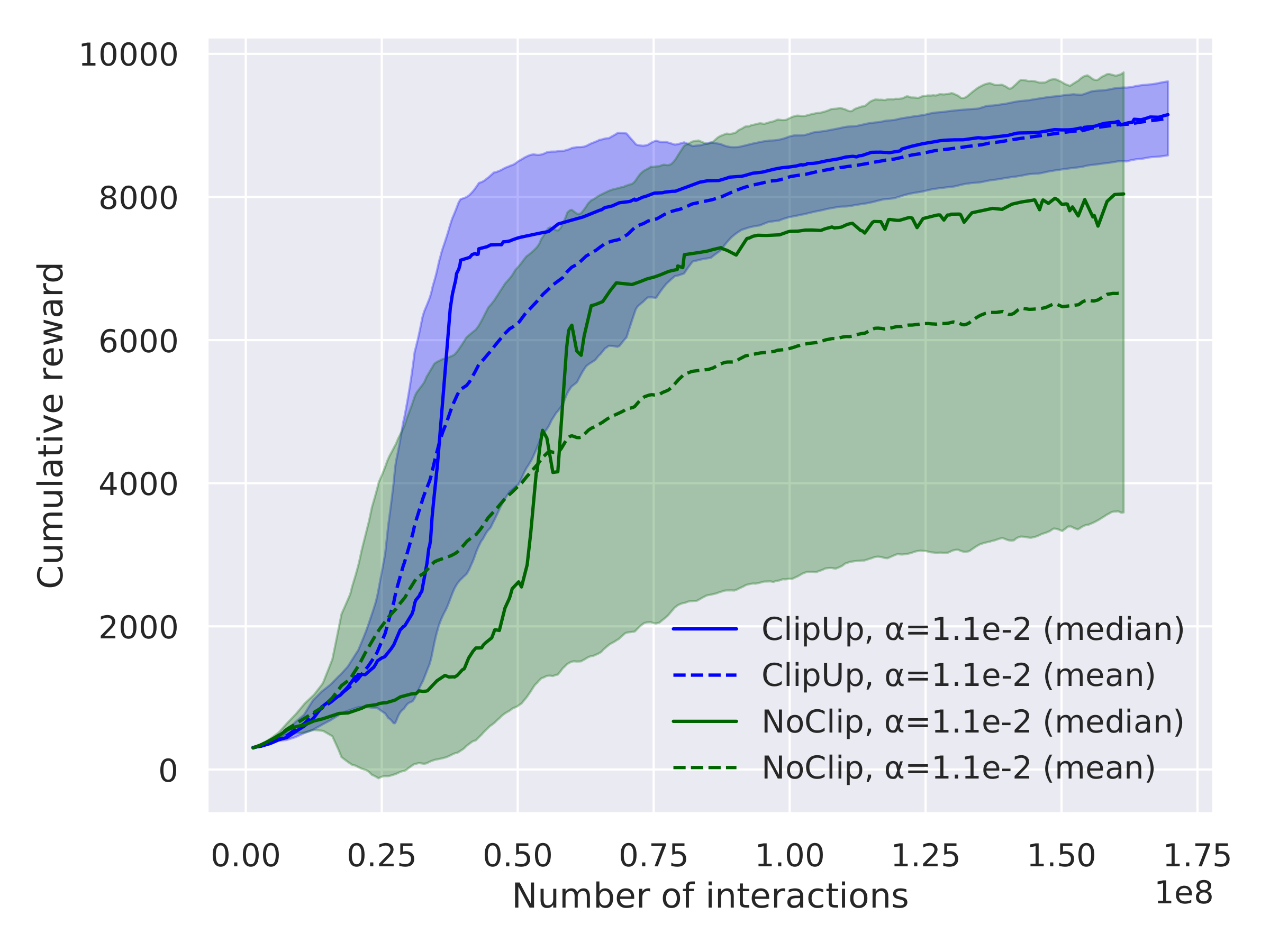
For further results and analysis, read our paper!

References

1. 1. Sehnke, Frank, Christian Osendorfer, Thomas Rückstieß, Alex Graves, Jan Peters, and Jürgen Schmidhuber. 2010. Parameter-exploring policy gradients. Neural Networks 23. Elsevier: 551–559.
2. 2. Mania, Horia, Aurelia Guy, and Benjamin Recht. 2018. Simple random search of static linear policies is competitive for reinforcement learning. In Advances in Neural Information Processing Systems, 1800–1809.
3. 3. Salimans, Tim, Jonathan Ho, Xi Chen, Szymon Sidor, and Ilya Sutskever. 2017. Evolution strategies as a scalable alternative to reinforcement learning. arXiv preprint arXiv:1703.03864.