Weighted Skip Connections are Not Harmful for Deep Nets
January 11, 2025
The paper Identity Mappings in Deep Residual Networks has design mistakes leading to incorrect conclusions about training deep networks with gated skip connections. You should try gated/weighted skip connections yourself and see if they improve results on your problems.
Before continuing, this should go without saying but in any case: This post is purely in the spirit of scientific discussion. I have deep respect for the authors’ many contributions to the field.
Side-note: I fully agree with Lucas’ side-take that OpenAI papers have been consistently the best at giving proper credit to past work among the big labs. I’ve often mentioned this in private but more people should acknowledge this publicly. A recent blog post by Lucas Beyer points readers to the paper Identity Mappings in Deep Residual Networks as playing a key role in the history of development of skip connections. Unfortunately, (partially) due to the mistakes made in this paper in comparing to Highway Networks, some researchers believe that ResNets are the only viable and scalable variant of HighwayNets, which were published earlier. Quick jump to the mistakes. Below are three experimental results as evidence that this is false.
Background
To begin, here’s the conclusion of the paper regarding messing with the shortcut or skip connections in its own words:
Multiplicative manipulations (scaling, gating, 1×1 convolutions, and dropout) on the shortcuts can hamper information propagation and lead to optimization problems.
… the degradation of these models is caused by optimization issues, instead of representational abilities.
This conclusion is supported by the following key figure from the paper:
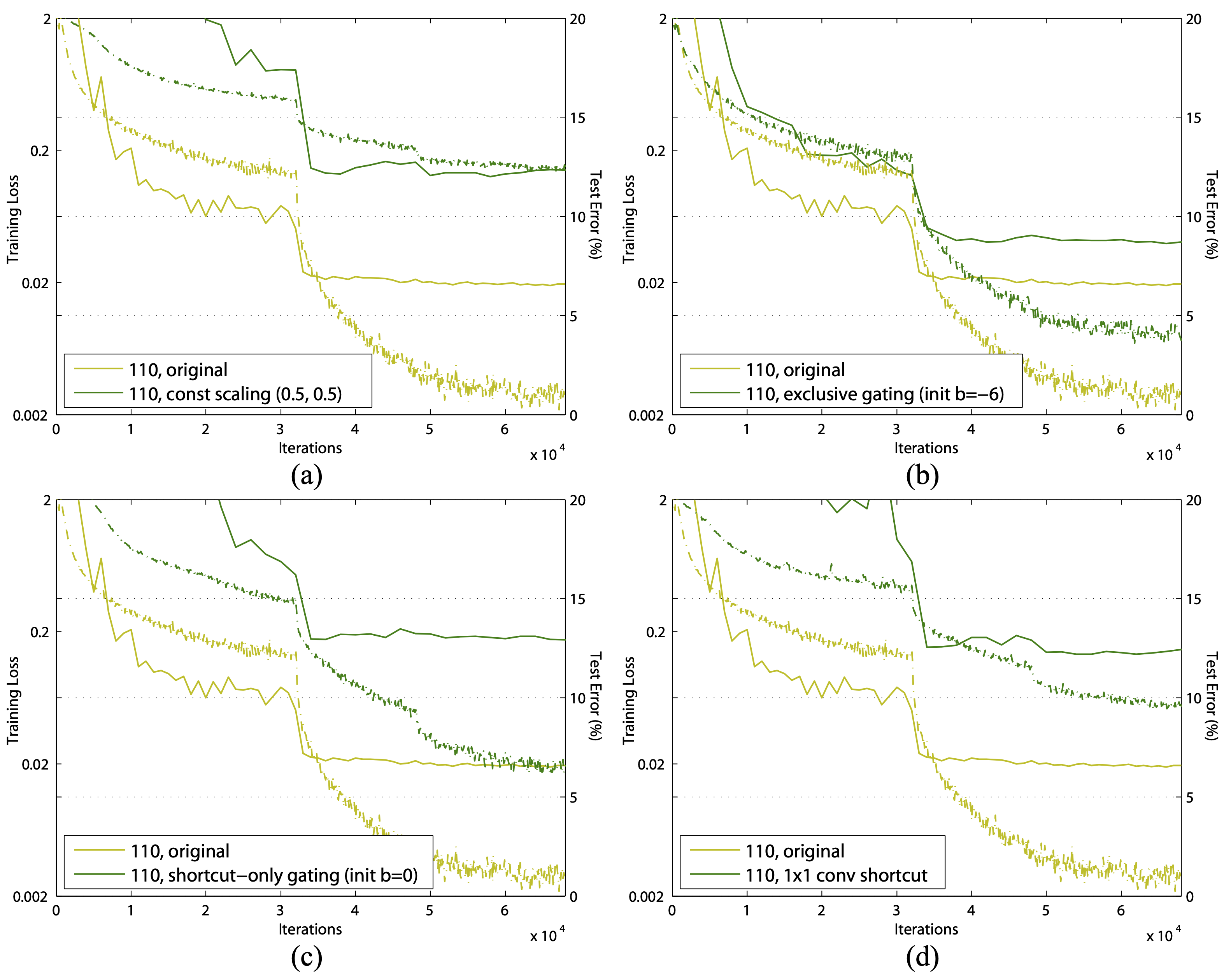
Focus on the top-right plot which compares Resnets to exclusive gating networks, which is the paper’s name for the design used by Highway Networks, the predecessor to Resnets.Quick summary: HighwayNets said “instead of the typical \(y=H(x)\) for a neural net layer, do \(y = H(x)T(x) + xC(x)\), where T and C are learnable gates. The variant of this used in experiments was \(H(x)T(x) + x(1 - T(x))\). ResNets said “do \(y=H(x) + x\)”. Clearly, the Resnet design leads to improved optimization (lower training loss) and hence a better final result on the test set (lower error rate), despite the fact that the gated network has more parameters (hence more computation) at its disposal. This, taken together with the other plots, does indeed support the conclusion regarding multiplicative manipulations on the shortcuts: they impede optimization and should be avoided!
The Mistakes

When comparing a proposed method to a previous method, one needs to implement the previous method correctly. This is where the mistakes happened, as highlighted in the figure above. If you read the Highway Networks papers, then this paper, you should ask: a) why are 1x1 convolutions used for the gates when the HighwayNets paper used the same function classes for \(H\) and \(T\)? b) why is an extra ReLU used after the addition which is absent in the HighwayNets papers? And finally, what happens if we remove these newly introduced elements? We arrive at the following design that follows the HighwayNets papers:
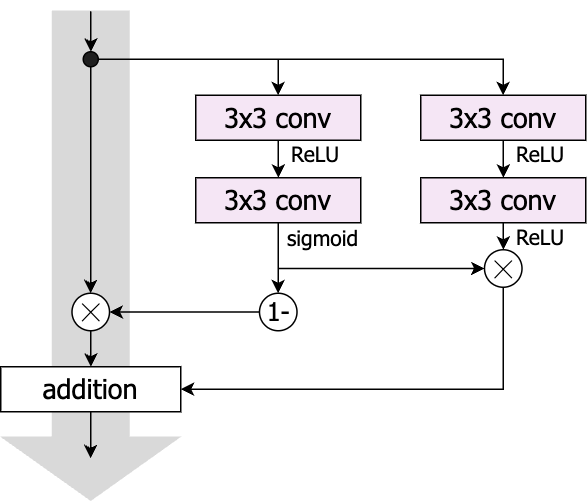
Evidence 1
Below is a new version of the top-right plot, this time following the design from the HighwayNets papers. We take the ResNet-v1, remove the final ReLU, and instead of 1x1 gates use the same receptive field and number of units as the non-identity path. The number of units in Highway layers is slightly reduced.The fact that the HighwayNet actually outperforms the ResNet can be explained by the fact that despite reducing the width by a factor of 0.875, it has more parameters. See notes & recommentations for a short discussion about this.
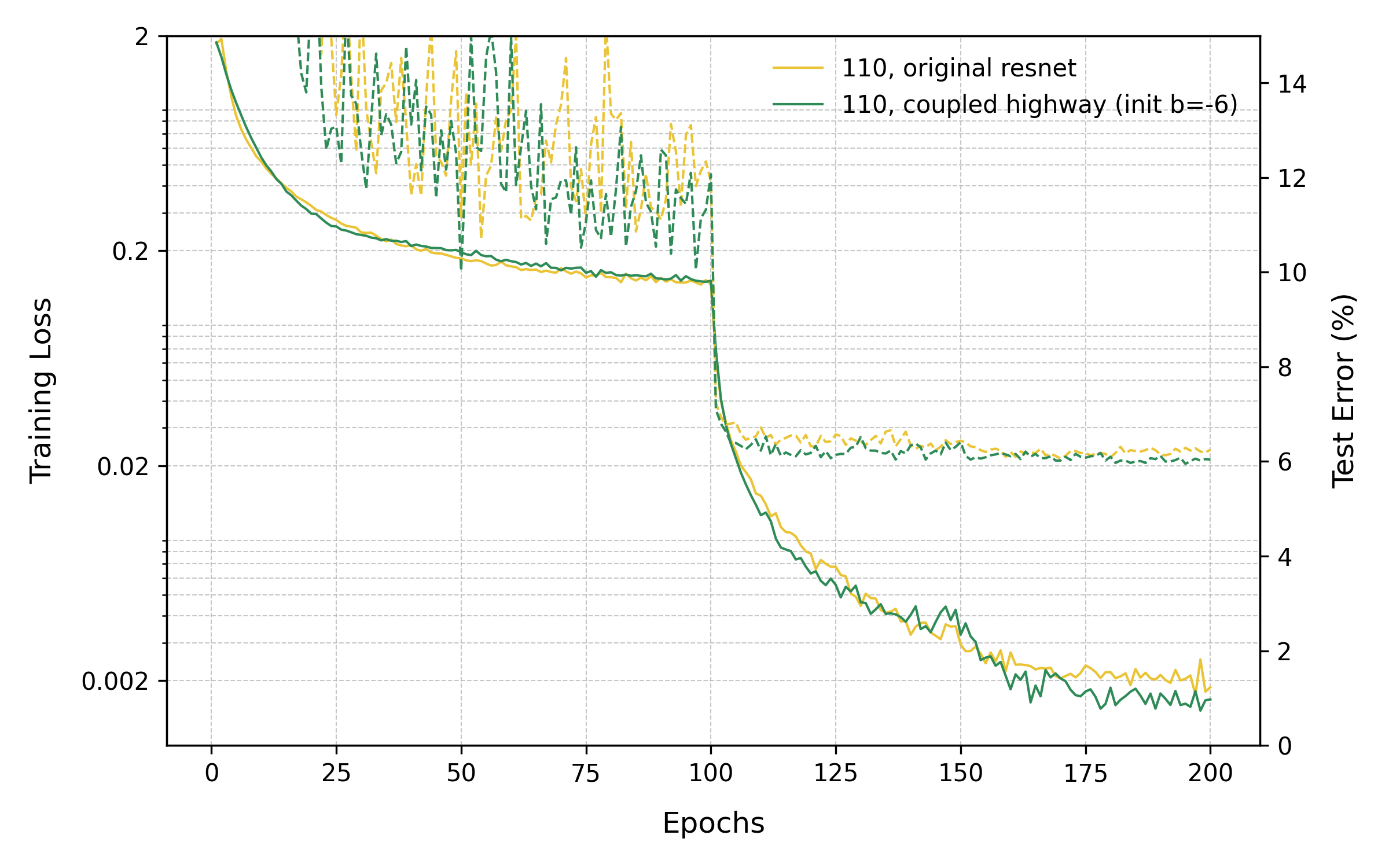
Clearly the optimization difficulties have disappeared, and gating does not seem to hamper the ability of the network to learn with over 100 layers. This directly contradicts the conclusion of the Identity Mappings paper that any manipulation of the shortcuts hurts information propagation. The design introduced by the paper to represent HighwayNets lead to poor training because the gates did not have enough information to learn when input signals should be transformed vs copied over.
If you’d like to reproduce these training curves, the code and logs are here. See more comparisons to see what happens if we remove the two changes one-by-one instead of together.
Evidence 2
This is just a pointer to already published results. In a follow-up paper on arXiv in 2016 (published in ICLR 2017), we discussed the same issue and showed the lack of optimization difficulties for 50-layer HighwayNets on ImageNet: see Section 5 [pdf link] of Highway and Residual Networks learn Unrolled Iterative Estimation. Unfortunately this paper is not very well known outside the small set of people interested in the iterative estimation view, so you are probably unfamiliar with it. In addition to these experiments, I think it has some cool ideas about the working of these deep networks, so check it out!
Evidence 3
When the excellent ResNet strikes back paper came out, I did similar experiments by directly converting ResNets to HighwayNets (with reduced widths) and running the improved training recipe A2 from the paper. The goal was to check if HighwayNets only work well for around 50 layers on ImageNet etc, and perhaps deeper nets on larger datasets require simple residual connections. Here are the results on the ImageNet val set:
| A1 (600 epochs) top-1 accuracy |
A2 (300 epochs) top-1 accuracy |
Parameters | Num. of Features | |
|---|---|---|---|---|
| ResNet50 | 80.4 | 79.8 | 25.5 M | 64, 128, 256, 512 |
| Highway50 | 80.3 | 26.4 M | 48, 96, 192, 384 | |
| ResNet101 | 81.5 | 81.3 | 44.5 M | 64, 128, 256, 512 |
| Highway101 | 81.8 | 44.2 M | 48, 96, 180, 384 | |
| ResNet152 | 82.0 | 81.8 | 60.2 M | 64, 128, 256, 512 |
| Highway152 | 82.3 | 59.9 M | 48, 96, 180, 384 |
Some observations:
HighwayNets consistently outperform ResNets with similar or slightly fewer number of parameters (but slightly more computation) and produce shorter representations (approx. 70%).
Highway50 trained with the A2 training recipe (300 epochs) exceeds performance of ResNet50 with A2 — 80.3% vs 79.8%. It almost matches the performance of Resnet50 with the A1 recipe (600 epochs) — 80.3% vs 80.4%. Note that typical variation across seeds is 0.1%.
Highway101 trained with A2 (300 epochs) exceeds performance of ResNet50 with A2 (300 epochs) — 81.8% vs 81.3%. It even outperforms Resnet101 trained with A1 (600 epochs), and matches ResNet152 trained with A2 at 81.8% top-1 accuracy.
Highway152 trained with A2 (300 epochs) outperforms ResNet152 trained with A2 (300 epochs) as well as A1 (600 epochs).
Overall, it does not seem to be the case that having gated shortcuts hampers learning. The code used for these experiments is here for completeness, though I have not run it since I did the experiments in 2021.
Notes & Recommendations
A related note is that the switch to a pre-activation design (proposed in this paper) was not needed for HighwayNets which did not have the post-activation design introduced by ResNets. Original HighwayNets were already often as trainable as pre-activation ResNets.Note that I’m referring to the location of the activation function, not that of the normalization layers. HighwayNets were developed towards end of 2014, mostly in parallel with BatchNorm, so they did not use normalization layers. Effectively combining normalization, bottleneck layers and skip connections was the key contribution of the ResNet paper. This is why HighwayNet in the second plot above does not need learning rate warmup which the original post-activation ResNet110 did.
Hopefully, I’ve convinced you that, at least with learnable gates, weighted skip connections do not hurt learning in general. Of course, successful network training depends on many many factors, so you may obtain different results in different situations. Nevertheless, I think there is enough evidence that you should experiment with weighted or gated skip connections for your problems, and see if they yield benefits in your situation.
When using gated skip connections, you should start by keeping the gates as “powerful” as the regular transformation. To control number of parameters, remember that HighwayNets can produce similar or better results with a smaller representation due to the use of dynamic multiplicative interactions not present in ResNets. Due to this, it is obviously not optimal to tune everything for a ResNet, and then just try to convert it to a HighwayNet, but even this often works reasonably well.Anecdotal example: for the HighwayNet110 above, a base learning rate of 0.2 instead of 0.1 turned out to perform even better in my experiments, compared to Resnet110. You should also try other variations, such as data-independent but learnable multiplicative connections, down-projections or weight-tying for efficient data-dependent gates, and of course the simplest residual skip connections.
More Comparisons and Subtleties
We saw above that the Identity Mappings paper introduced two “breaking” changes to HighwayNets: the transform gate only used a single layer of 1x1 convolutions, and a “post-activation” design meaning that the activation function was applied after the addition shortcut. Let’s check what happens if we start with the “breaking” model from the paper and only roll-back one of these changes at a time, instead of both together.
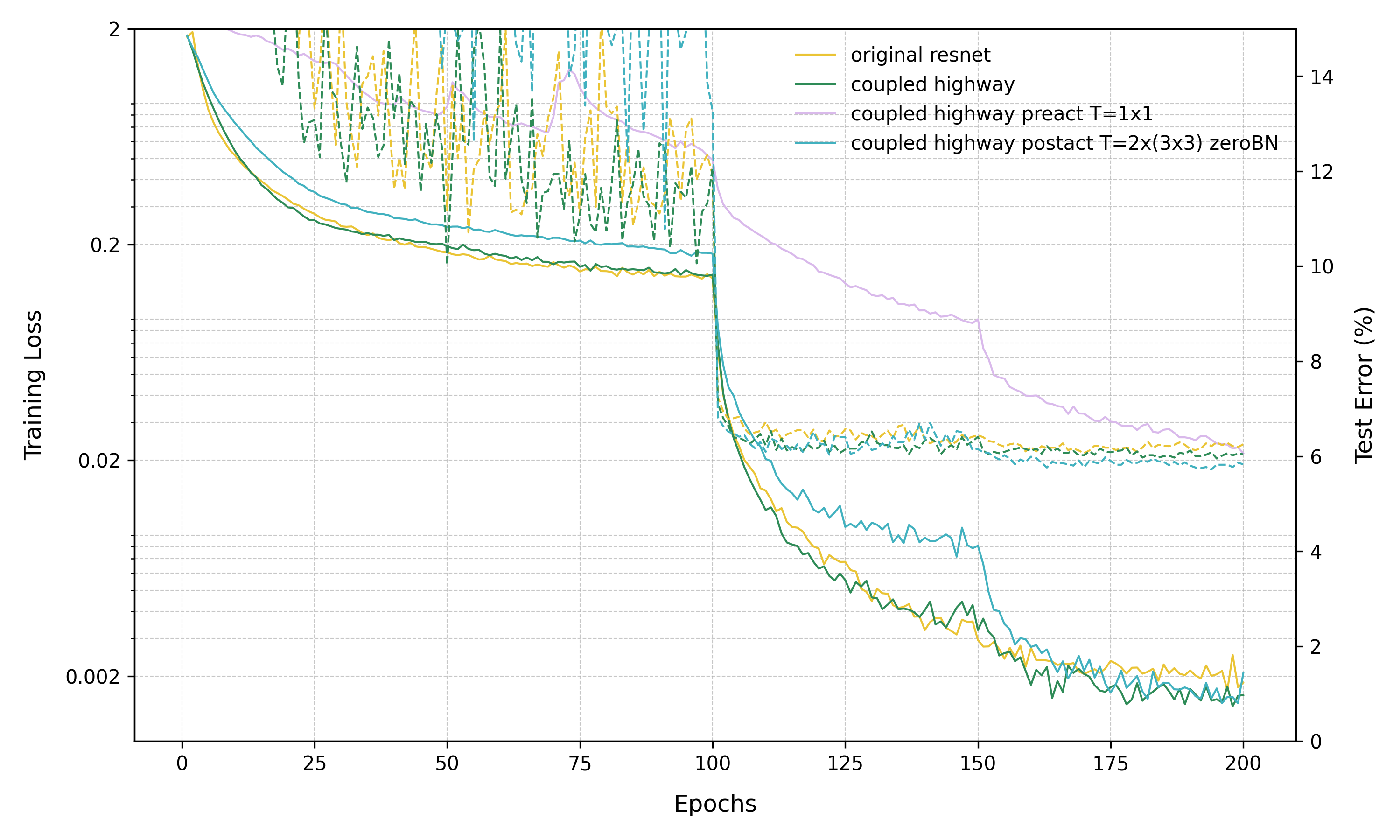
We have not re-tuned hyperparameters or initialization scales, so this will be just a quick test. I think this is not a critical limitation in this particular case, so we learn a few things from this experiment and the resulting plot above.
If we switch to pre-activation but still use a single 1x1 conv to learn the gating (preact T=1x1), then the model trains very poorly.
If we instead keep post-activation but switch to two 3x3 conv layers to learn the gating (postact T=2x(3x3) zeroBN), then the model both fits the data (training loss) and generalizes (test error) well.
But what is this zeroBN?
Turns out postact T=2x(3x3) becomes extremely unstable to train.
One way to tackle this would be to change the initialization of the conv layers, but there’s a simpler fix.
We can initialize the non-residual transformation to produces zeros by zero-ing out the weights of the last normalization layer in that path.
This trick is commonly used by practitioners, particularly in computer vision, so it’s nothing new but completely solves the instability issues resulting in the plot above.
Incidentally, it was also used by ResNet Strikes Back, which is why all the results in Evidence 3 above are with a post-activation design.
I really like this result because it is a nice reminder of the subtleties involved in architecture comparison: non-architecture choices strongly affect architecture comparisons. This has long been one of the most important things to remember in deep learning research.
Further Reducing Parameters
The HighwayNet110 used for Evidence 1 above has 2.6M parameters, while ResNet110 has 1.7M. Does it perform better only because of this? No. In fact, the Identity Mappings paper explicitly notes that having more parameters does not help because the issue at hand is worse optimization due to depth. In their experiments, the exclusive gating network does not train well despite having more parameters, so this is not about parameter count.
Nevertheless, beyond the subject of depth, parameter count or computational efficiency are important to consider. On this, remember that “HighwayNets use twice as many parameters as ResNets” would be very naïve, because that’s not how architectures are compared.How I wish it was that easy … In the CIFAR-10 example above, even though I was doing the (suboptimal) thing by just taking a heavily tuned ResNet and just converting it to HighwayNet, I reduced the width of all blocks by a factor of 0.875.
Similarly, for the ImageNet experiments, I reduced the widths by a factor of around 0.75 or 0.7. This lead to nets that still took some more wall-time to train as I recall, but obtained much shorter representations, which might be very important for many applications! For a new problem, if you experiment with gated/weighted nets in general instead of tuning everything to ResNets, you can obtain a net that works well and is efficient for your needs.
As a very simple illustrative example, let’s look at the 2.6M HighwayNet110 on CIFAR-10 a bit. If we reduce the width multiplier factor below 0.875 to further reduce parameters, we seem to obtain a small degradation in results – why might that be? Well, the reason is that ResNet-110 was already skinny: 16, 32, 64 units in the three stacks of blocks, which reduces to 14, 28, 56 with a factor of 0.875. At some point the size of the representations we are working with is getting too small. What happens if we use 16, 24, 48 units, and add a convolution layer at the end to project back to 64 feature maps? We obtain HighwayNet111 that now has 1.97M parameters, but produces similar train loss and test accuracy as before.
Acknowledgement
Thanks a lot to Lucas Beyer for very helpful comments and suggestions to improve this post!